
UNIT CIRCLE SPECIAL RIGHT TRIANGLES HOW TO
UNIT CIRCLE SPECIAL RIGHT TRIANGLES FREE
We won't describe it here, but feel free to check out 3 essential tips on how to remember the unit circle or this WikiHow page. Wherever possible, we'd like to be able to identify the exact height of a given point on the unit circle. The other part - remembering the whole unit circle chart, with sine and cosine values - is a slightly longer process. Also, since xcos and ysin, we get: (cos()) 2 + (sin()) 2 1 a useful 'identity' Important Angles: 30°, 45° and 60°. Special angle-based triangles inscribed in a unit circle are handy for. Pythagoras Theorem says that for a right angled triangle, the square of the long side equals the sum of the squares of the other two sides. For any other angle, you can use the formula for angle conversion:Ĭonversion of the unit circle's radians to degrees shouldn't be a problem anymore! 💪 For example, a right triangle may have angles that form simple relationships. You know how to find the side lengths for special right triangles (30-60-90 and 45-45-90) given one side, and as /630 degrees, this triangle is one of those special cases. Start by drawing the angle /6 on the unit circle. The most important angles are those that you'll use all the time:Īs these angles are very common, try to learn them by heart ❤️. Find and memorize the 6 trig functions of the special angle /6. Each black-and-red (or black-and-yellow) triangles is a special right-angled.

The trigonometric functions of the popular angles. How do the Special Right Triangles relate to the Unit Circle CJ Marland 2007.
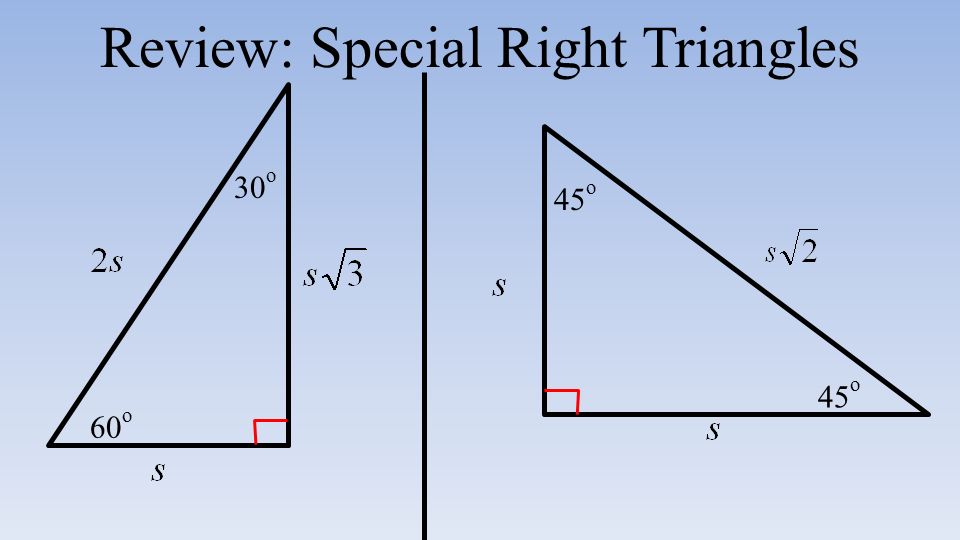
The proof is given by the Pythagoras theorem.įrom the basic concept we know that the Pythagoras theorem states that the square of the longest side that is the hypotenuse is equal to the sum of the squares of the other two adjacent sides in a right angle triangle.įrom the below represented figure, we can explain the relation between special right triangles and a unit circle.Well, it depends what you want to memorize 🙃 There are two things to remember when it comes to the unit circle:Īngle conversion, so how to change between an angle in degrees and one in terms of π (unit circle radians) and Type \: Triangle that has its side measures in the ratio of \. Type \: Triangle that is half of an equilateral triangle. As the special right triangles are inscribed in quadrants 2, 3, and 4, the legs of the triangles take on values to reflect the direction taken in order for the radius (hypotenuse) to intersect the critical value on the unit circle.

There are two types of special right triangles. First of all, we have to know about the special right triangles and unit circle. Hint: From the question given, we have been asked to relate the special right triangles to the unit circle. Because of the relationships found in special right triangles (see diagrams), the coordinates of the points on the unit circle for angles of rotation that are multiples of 4 (or 45 °), 6 (or 30 °), and 3 (or 60 °) can be labeled with exact values, such as shown for the first quadrant of the unit circle diagram.


 0 kommentar(er)
0 kommentar(er)
